Inference in deep learning
There are many, many new generative methods developed in the recent years.
- denoising autoencoders
- generative stochastic networks
- variational autoencoders
- importance weighted autoencoders
- generative adversarial networks
- infusion training
- variational walkback
- stacked generative adversarial networks
- generative latent optimization
- deep learning through the use of non-equilibrium thermodynamics
Deep Models
We can’t delve into the details of those old workhorse models, but let us summarize a few of them nevertheless.
A Boltzmann machine can be seen as a stochastic generalization of a Hopfield network. In their unrestricted form Hebbian learning is often used to learn representations.
A restricted Boltzmann machine, or Harmonium, restricts a Boltzmann machine in the sense that the neurons have to form a bipartite graph. Neurons in one “group” are allowed connections to another group, and the other way around, but they are not allowed to be connected to neurons in the same group. This restriction naturally, but not necessarily leads to structures that resemble layers.
A deep belief network hand deep Boltzmann machines have multiple (hidden) layers that are each connected to each other in the restricted sense of above. These models are basically stacks of restricted Boltzmann machines. This is by the way only true in a handwaving manner. A deep belief network is not a true Boltzmann machine because its lower layers form a directed generative model. Salakhutdinov and Hinton (pdf) spell out the differences in detail.
Markov Chain Monte Carlo (MCMC)
Restricted Boltzmann Machines, Deep Belief Networks, and Deep Boltzmann Machines were trained by MCMC methods. MCMC computes the gradient of the log-likelihood (see post on contrastive divergence. MCMC has particular difficulty in mixing between modes.
Autoencoder
An autoencoder has an input layer, one or more hidden layers, and an output layer. If the hidden layer has fewer nodes than the input layer it is a dimension reduction technique. Given a particular input, the hidden layer represents only particular abstractions that are subsequently enriched so that the output corresponds to the original input. An other dimension reduction technique is for example principle component analysis which has some additional constraints such as linearity of the nodes. Given the shape an autoencoder can also be called a bottleneck or sandglass network.
If we represent the encoder \(F: X \rightarrow H\) and the decoder \(G: H \rightarrow X\). We apply the individual \(x\) to the product as \(x' = (G \circ F)x\), then we can define the autoencoder as:
\[\{F, G \} = \arg \min_{F,G} \| X - X'\|^2\]Here we choose for an L2 norm for the reconstruction: \(L(x,x') = \| x-x' \|^2\).
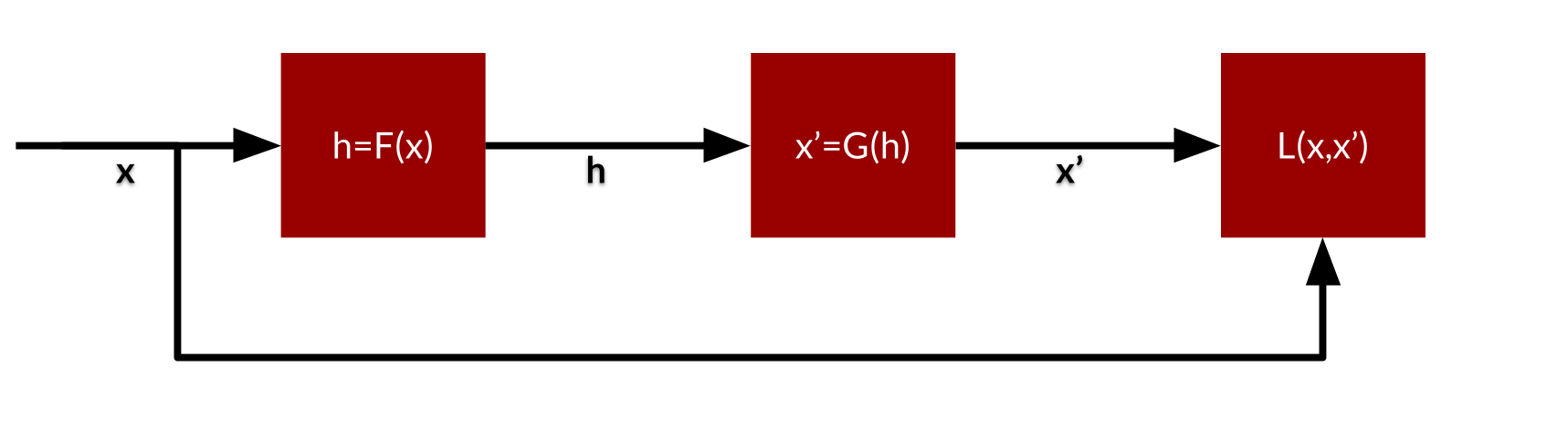
An autoencoder is typically trained using a variant of backpropagation (conjugate gradient method, steepest descent). It is possible to use so-called pre-training. Train each two subsequent layers as a restricted Boltzmann machine and use backpropagation for fine-tuning.
A nice blog post at Keras explains also some of the disadvantages of autoencoders, a very clarifying read!
Denoising Autoencoders
A denoising autoencoder (DAE) is a regular autoencoder with the input signal corrupted by noice (on purpose: \(\tilde{x} = B(x)\)). This forces the autoencoder to be resilient against missing or corrupted values in the input.
The reconstruction error is again measured by \(L(x,x') = \| x - x'\|^2\), but now \(x'\) is formed by a distortion of the original \(x\), denoted by \(\tilde{x}\), hence \(x' = (G \circ F) \tilde{x}\).
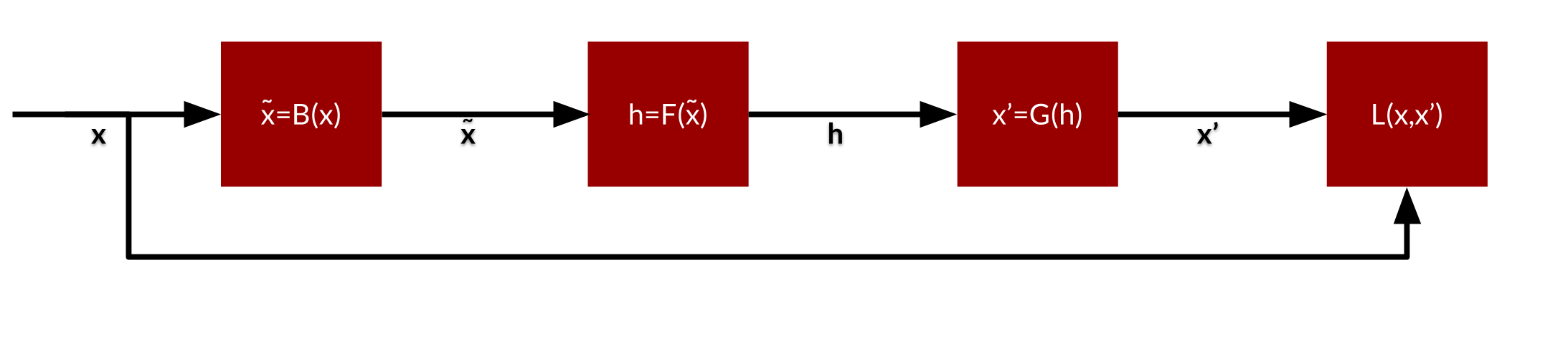
Note that a denoising autoencoder can be seen as a stochastic transition operator from input space to input space. In other words, if some input is given, it will generate something “nearby” in some abstract sense. An autoencoder is typically started from or very close to the training data. The goal is to get an equilibrium distribution that contains all the modes. It is henceforth important that the autoencoder mixes properly between the different modes, also modes that are “far” away.
Variational Autoencoders
The post by Miriam Shiffman is a nice introduction to variational autoencoders. They have been designed by (Kingma and Welling, 2014) and (Rezende et al., 2014). The main difference is that \(h\) is now a full-fledged random variable, often Gaussian.
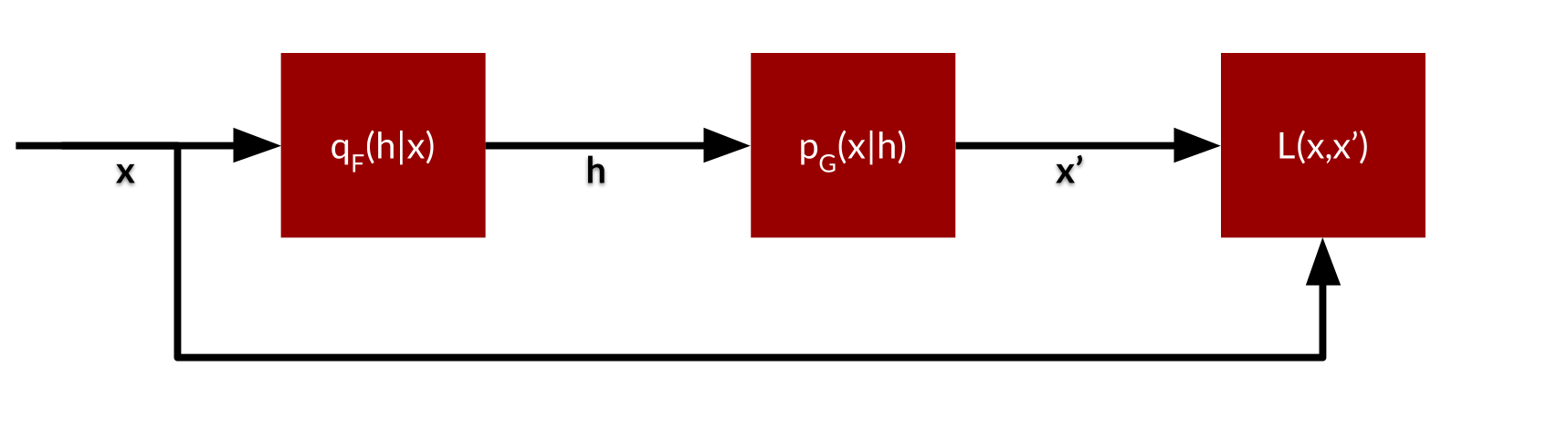
A variational autoencoder can be seen as a (bottom-up) recognition model and a (top-down) generative model. The recognition model maps observations to latent variables. The generative model maps latent variables to observations. In an autoencoder setup the generated observations should be similar to the real observations that go into the recognition model. Both models are trained simultanously. The latent variables are constrained in such a way that a representation is found that is approximately factorial.
Helmholtz Machine
A Helmholtz machine is a probabilistic model similar to the variational autoencoder. It is trained by the so-called sleep-wake algorithm (similar to expectation-maximization).
Importance weighted Autoencoders
The importance weighted autoencoder (Burda et al., 2015) is similar to the variational autoencoder, but it uses a tighter loglikelihood lower bound through applying importance weighting. The main difference is that the recognition model uses multiple samples (to approximate the posterior distribution over latent variables given the observations). In order words, the recognition model is run a few times and the suggested latent variables are combined to get a better estimate. The model gives more weight to the recognition model than the generative model.
\[\mathcal{L}(x) = \mathbb{E}_{z \sim q(z|x) } \left[ \log \frac{1}{k} \sum_k \frac{p(x,z)}{q(z|x)} \right]\]Generative Adversarial Networks
Generative Adversarial Networks (Goodfellow et al., 2014) use two networks. A generative model \(G\) and a discriminative model \(D\). The generative model maps latent variables \(z\) to data points \(x'\). The discriminator has to make a choice between true data \(x\) and fake data \(x'\). Hereby should \(D(x)\) have a large value and \(D(x')\) have a small value. The discriminator maximizes (we fix the generator):
\[V(D) = \mathbb{E}_{x\sim p_{data}(x)} \left[ \log( D(x) \right] + \mathbb{E}_{x' \leftarrow G(z)} \left[ \log( 1 - D(x') \right]\]The generator in contrast maximizes:
\[V(D,G) = \mathbb{E}_{x\sim p_{data}(x)} \left[ \log( D(x) \right] + \mathbb{E}_{z \sim G(z)} \left[ \log( 1 - D(G(z)) \right]\]It is clearly visualized by Mark Chang’s slide.
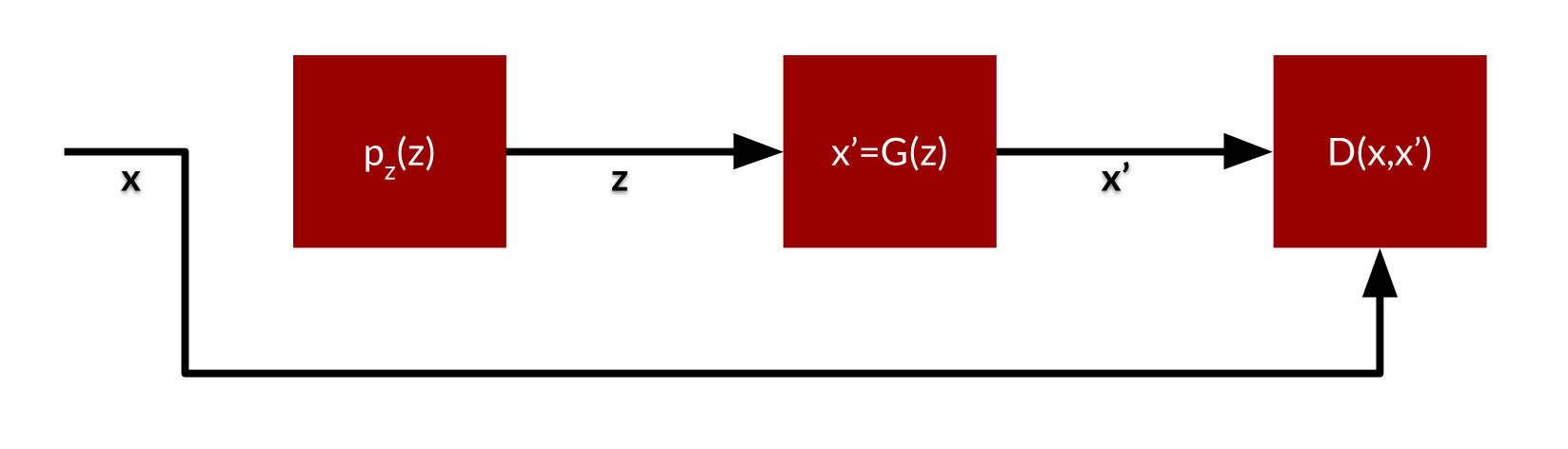
The distribution \(p_z(z)\) is a arbitrary noise distribution. In other words, the generator morphs totally random stuff into meaningful \(x\). It is like throwing darts randomly into a dart board and the generator folding the board into a hat. Similarly from pure random values we can draw point clouds that have elaborate structure.
The latent variables \(z\) are totally random, however there is something else important here. If \(z\) is a multidimensional random variable information across all dimensions can be used to construct \(x' \leftarrow G(z)\). There is no information about \(z\) if we would like to reason back from \(x'\). This means that from a representation learning perspective the unconstrained use of \(z\) leads to entangled use of it in \(G\). InfoGAN introduces an additional mutual information term between a latent code \(C\) and generated data \(X\).
Adversarial Autoencoders
Adversarial Autoencoders (Makhzani et al., 2016) is an autoencoder that uses generative adversarial networks. The latent variables (the code) are matched with a prior distribution. This prior distribution can be anything. The autoencoder subsequently maps this to the data distribution.
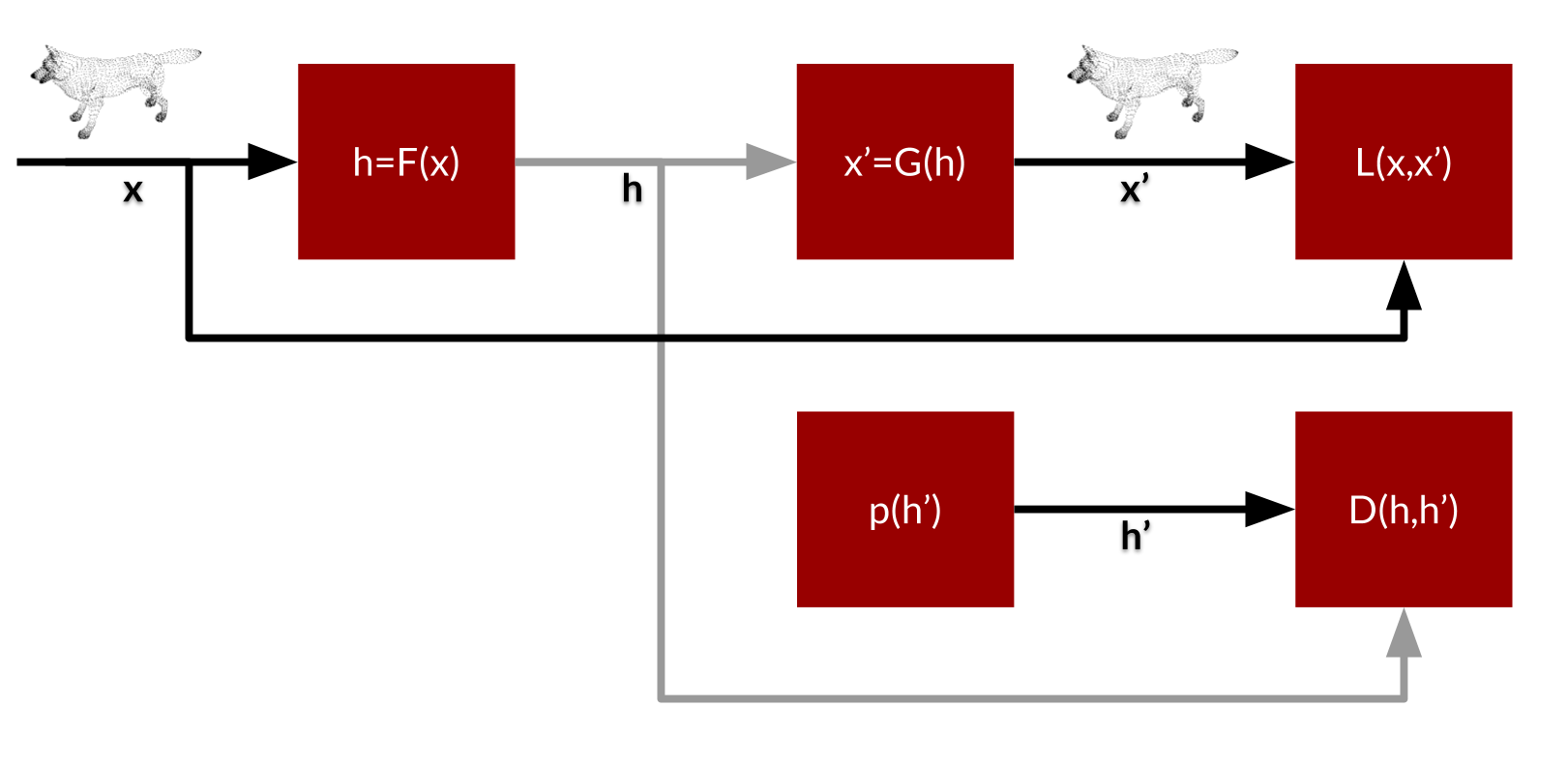
Note that the use of the adversarial network is on the level of the hidden variables. The discriminator attempts to distinguish “true” from “fake” hidden variables.
This immediately rises the following question: Can we also generate fake data as well? If one discriminator has the goal to distinguish true from fake hidden variables, the other can have as goal to distinguish true from fake data. We should take provisions to not have the former discriminator punished by a bad performing second discriminator.
Deep Learning Through The Use Of Non-Equilibrium Thermodynamics
Non-equilibrium Thermodynamics (Sohl-Dickstein et al., 2015) slowly destroys structure in a data distribution through a diffusion process. Then a reverse diffusion process is learned that restores the structure in the ata.
Both processes are factorial Gaussians, the forward process, \(p(x^{t}\mid p(x^{t-1})\) and the inverse process, \(p(x^{t-1}\mid p(x^t)\).
To have an exact inverse diffusion the chain requires thousands of small steps.
Infusion Training
Infusion training (Bordes et al., 2017) learns a generative model as the transition operator of a Markov chain. When applied multiple times on unstructured random noise, infusion training will denoise it into a sample that matches the target distribution.

Variational Walkback
Variational Walkback (Goyal et al., 2017) learns a transition operator as a stochastic recurrent network. It learns those operators which can represent a nonequilibrium stationary distribution (also violating detailed balance) directly. The training objective is a variational one. The chain is allowed to “walk back” and revisit states that were quite “interesting” in the past.
Compared to MCMC we do not have detailed balance, nor an energy function. A detailed balance condition would by the way mean a network with symmetric weights.
Nonparametric autoencoders
The latent variables in the standard variational autoencoder are Gaussian and have a fixed quantity. The ideal hidden representation however might require a dynamic number of such latent variables. For example if the neural network has only 8 latent variables in the MNIST task it has to somehow represent 10 digits with these 8 variables.
To extend the hidden layer from a fixed to a variable number of nodes it is possible to use methods developed in the nonparametric Bayesian literature.
There have been already several developments:
- A stick-breaking variational autoencoder (Nalisnick and Smyth, 2017) where the latent variables are represented by a stick-breaking process (SB-VAE). The inference is done using stochastic gradient descent, which requires a representation where the parameters of a distribution are separated from an independent stochastic noise factor, called a differentiable, non-centered parametrization (DNCP). With a Gaussian distribution this is done through the reparameterization trick (see below). For a stick-breaking process Beta random variables need to be sampled. This can be done by drawing \(x \sim Gamma(\alpha,1)\) and \(y \sim Gamma(\beta,1)\) and have \(v = x/(x+y)\), corresponding to \(v \sim Beta(\alpha,\beta)\). This does not work as a DNCP though, because Gamma does not have one w.r.t. the shape parameter. When close to zero an inverse CDF might be used. However, the authors opt for a so-called Kumaraswamy distribution;
- A nested Chinese Restaurant Process as a prior on the latent variables (Goyal et al., 2017);
- An (ordinary) Gaussian mixture as a prior distribution on the latent variables (Dilokthanakul et al., 2017), but see this interesting blog post for a critical review (GMVAE);
- A deep latent Gaussian mixture model (Nalisnick et al, 2016) where a Gaussian mixture is used as the approximate posterior (DLGMM);
- Variational deep embedding uses (again) a mixture of Gaussians as a prior (Jiang et al., 2017) (VaDE);
- Variational autoencoded deep Gaussian Processes (Dai et al., 2016) uses a “chain” of Gaussian Processes to represent multiple layers of latent variables (VAE-DGP).
The problem with autoencoders is that they actually do not define how the latent variables are to be used.
Inherently, without additional constraints the representation problem is ill-posed. Suppose for example that the generator is just a dictionary of images and that training will make the latent variables point to a particular index in this dictionary. In this way no deep structure has been uncovered by the network at all. It’s pretty much just pointing at what it has been seen during training. Generalization can be expected to be pretty bad.
Especially when variational autoencoders are used in sequence modeling it becomes apparent that the latent code is generally not used. The variational lossy autoencoder introduces control over the latent code to successfully combine them with recurrent networks (Chen et al., 2017).
From an information-theoretic perspective the differences can be formulated in an extreme manner: maximization or minimization of mutual information. With InfoGAN (not explained in this blog post) mutual information between input and latent variables is maximized to make sure that the variables are all used. This is useful to avoid the “uninformative latent code problem”, where latent features are actually not used in the training. However, with for example the information bottleneck approach the mutual information between input and latent variables is minimized (under the constraint that the features still predict some labels). This makes sense from the perspective of compression. This behavior can all be seen as a so-called information-autoencoding family (Zhao et al., 2017).
It is interesting to study how nonparametric Bayesian methods fare with respect to this family and what role they fulfill in such a constrained optimization problem. Existing models namely use fixed values for the Lagrangian multipliers (the tradeoffs they make).
Mode Collapse
There are several research directions where mode collapse is the main topic. Mode collapse is especially prevalent in generative adversarial networks. In distributional adversarial networks (Li et al., 2017) two adversaries are defined that are slightly different from the normal one, both based on a so-called deep mean encoder. The deep mean encoder has the form:
\[\eta(P) = \mathop{\mathbb{E}}_{x \sim P} [ \phi(x) ]\]The GAN objective function is:
\[\min_G \max_D { \mathop{\mathbb{E}}_{x \sim P_x} [ \log D(x) ] + \mathop{\mathbb{E}}_{z \sim P_z} [ \log (1 - D(G(z)) ] }\]The authors extend it with an additional term:
\[\min_G \max_{D,M} { \lambda_1 \mathop{\mathbb{E}}_{x \sim P_x} [ \log D(x) ] + \mathop{\mathbb{E}}_{z \sim P_z} [ \log (1 - D(G(z)) ] + \lambda_2 M(P_x,P_G) }\]The sample classifier \(\psi\) uses the above intermediate summary statistics \(\eta(P)\) to define a costs (it outputs 1 if sample is drawn from \(P_x\) and 0 otherwise).
\[M(P_x,P_G) = { \log \psi (\eta (P_G)) ] + \log (1 - \psi (\eta(P_x)) ] }\]Generalization
The GAN objective:
\[\min_{u \in U} \max_{v \in V} { \mathop{\mathbb{E}}_{x \sim D_{real}} [ \phi ( D_v(x) ) ] + \mathop{\mathbb{E}}_{x \sim D_{G_u}} [ \phi (1 - D_v(x)) ] }\]This objective assumes we have an infinite number of samples from \(D_{real}\) to estimate \(\mathop{\mathbb{E}}_{x \sim D_{real}} [ \phi ( D_v(x) ) ]\). If we have only a finite number of training examples \(x_1, \ldots, x_m \sim D_{real}\), we use the following to estimate this expectation: \(\frac{1}{m} \sum_{i=1}^m [ \phi(D_v(x))]\).
Regularization
Training deep networks has undergone several advances. One of the first innovations has been the layer by layer training. Other concepts you will find are:
- dropout
- stochastic gradient descent
- batch normalization
- residual training
- reparameterization trick
We will briefly describe them, but they each easily deserve a dedicated explanation as well. So little time!
Dropout
Another key idea has been to randomly drop units including connections during training. This prevents overfitting. During training in this way a collection of differently thinned networks is used. At testing an unthinned network is used. This is called dropout (Srivastava et al., 2014).
Stochastic gradient descent
Gradient descent or steepest descent is an iterative method where we take steps that depend on the slope (or more general, that depend on the gradient) with as purpose to end up at a minimum. To get (negative) gradients we need to have differential functions.
Stochastic gradient descent is a stochastic approximation to gradient descent. What is approximated is the true gradient. Adjusting the parameters \(\theta\) it minimizes the following loss function:
\[\theta = \arg \min_\theta \frac{1}{N} \sum_{i=1}^N L(x_i;\theta)\]Here \(x_1, \ldots x_N\) is the training set. Stochastic gradient descent now incrementally navigates to the values for $\theta$ where the sum over the function $L(x_i, \theta)$ is minimized. The parameter $\theta$ is continuously adjusted by looping over all observations $x_i$:
\[\theta' = \theta - \eta \frac{\partial }{\partial \theta} L(x_i;\theta)\]After looping over all observations, stochastic gradient descent performs this loop again and again till some kind of convergence criterion is met or until the researcher likes to have a beer, read a book, or spend time on social media.
Batch normalization
The distribution of network activities change during training due to the fact that the network parameters change. This phenomenon is called internal covariate shift. It is possible to fix the distribution of the layer inputs \(x\) as the training progresses. It is for example well-known that whitening the inputs (linear transforming them to zero means, unit variances and decorrelating them) makes a network converge faster. Batch normalization does not simply whiten each layer’s input, but makes two simplifications: (1) normalize each scalar feature independently, and (2) introduce scale and shift parameters to preserve nonlinearities. Batch normalization improved significantly on the ImageNet classification task (Ioffe and Szegedy, 2015).
Residual learning
Making networks deeper and deeper counterintuitively increases the training error and thus the test error. Consider for example an identity mapping (as with autoencoders): a network needs to learn to duplicate the input to generate the output. Empirical evidence shows that learning the difference (in this case zero between input and output) is easier for a network. This is called residual learning (He et al., 2015. At ImageNet such residual nets achieve 3.57% error on the test set. It is hence no surprise that the fourth edition of the Inception networks use residual learning (Szegedy et al., 2017).
Reparameterization Trick
The reparameterization trick replaces a (blackbox) stochastic node in a computational graph with a node that is non-stochastic (of which a gradient can be calculated) with the noise added separately. It’s just as if the salt is added after you have made the soup. It substitutes a random variable by a deterministic transformation of a simpler random variable. There are three popular methods (Shakir Mohammed blog):
- Inverse sampling. The inverse cumulative distribution function can be used as the transformation.
- Polar methods. Generating pairs (e.g. the basis of the Box-Muller transform).
- Coordinate transformation methods (shifting and scaling).
The last example uses the fact that the transformation ($x = g(\epsilon;\theta)$) is valid for particular well chosen one-liners:
\[\frac{\partial}{\partial \theta} \sum_{i=1}^N p(x_i; \theta) f(x_i) = \frac{\partial}{\partial \theta} \sum_{i=1}^N p(\epsilon_i) f(g(\epsilon_i;\theta))\]For example the (zero-centered) Normal distribution is defined as:
\[p(x;\theta) = N(0,\theta)\]We can write this as a standard Normal distribution with a deterministic transformation:
\[p(\epsilon) = N(0,1)\] \[g(\epsilon; \theta) = \theta \epsilon\]The result is that through this reparameterization the variance can be substantially reduced (potentially!). The reparameterization trick is well explained by Goker Ergodan in this Jupyter notebook.